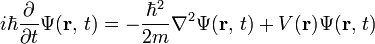在物理圈圈打滾6年後,終於發現幾件關於量子物理的事情。初學者一定知道,我們對於Schrödinger eq. 為什麼能夠這麼重要,實在是摸不著頭緒。經過一整個禮拜的推敲,我找到一個令我滿意的說法......是這樣的:
首先,我們要"準備"一個系統。在對這個系統施做任何事情之前,我們要能夠用想的來推測它的狀態(也就是初始狀態)是什麼。所以我們所要準備的事物是「系統本身」、「環境」以及推測系統狀態的方法。透過數學,物理學家們把「系統本身」、「環境」寫進Schrödinger Equation中,並求其解,來理解系統的初始狀態,並以 initial state wave function 來表示系統初始狀態。
然後才能對系統做量測,得到某個確定的物理量的同時,initial state wave function 也會縮簡為某個特定的state wave function。透過數學,我們得知一種特殊的方程式:Eigenvalues equation,可以完整的描述這個物理過程。Schrödinger Equation正屬於Eigenvalues equation。以下,我以流程簡圖來表示這整個過程。
| [系統本身 + 環境(位能) + Schrödinger equation] 解方程式,可得N組 (eigenvalue, eigensolution)。 將這N個eigensolutions 以線性組合的方式,合成一個"Schrödinger equation的通解",也就是 initial state wave function. | |
|| || ︾ | 實施 measurement,得到能量 = Em. |
| 量測後的系統態是一個特定的eigenstate。換句話說:「量測」這個動作,把系統初始態變成一個 eigenstate (對應於我們測得的能量 Em 的系統態) | |
|| || ︾ | 實施第二次measurement,得到相同的能量 = Em. |
| 系統維持在同一個 eigenstate. 所以此eigenstate的出現機率=100% | |
總而言之:
- 關於Measurement的數學表示我仍不清楚。
- Schrödinger equation 其實是用來計算系統總能和系統波函數的一個 eigenvalues equation;然而,因為系統波函數剛好包含了關於系統的完整資訊,所以,Schrödinger equation 才得以成為量子物理的核心。